[Programmers] 산 모양 타일링

문제

프로그래머스-산 모양 타일링

문제 풀이

이 문제는 사다리꼴에 정삼각형을 붙인 모양에 타일을 배치하는 경우의 수를 구하는 문제이다.

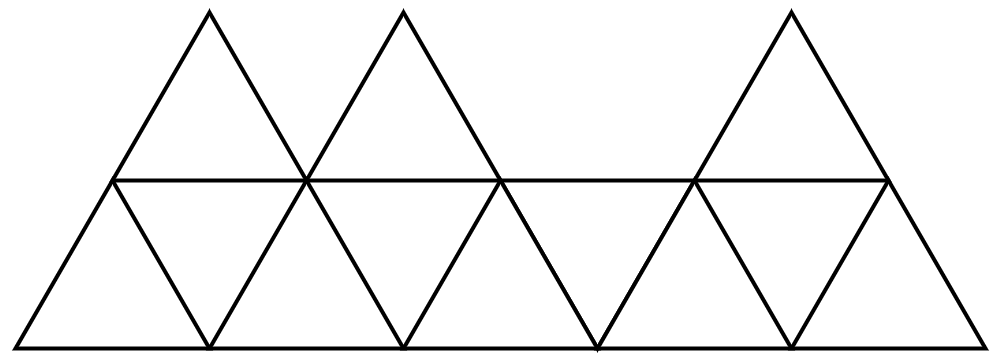
이 그림에서 밑은 다음과 같다.

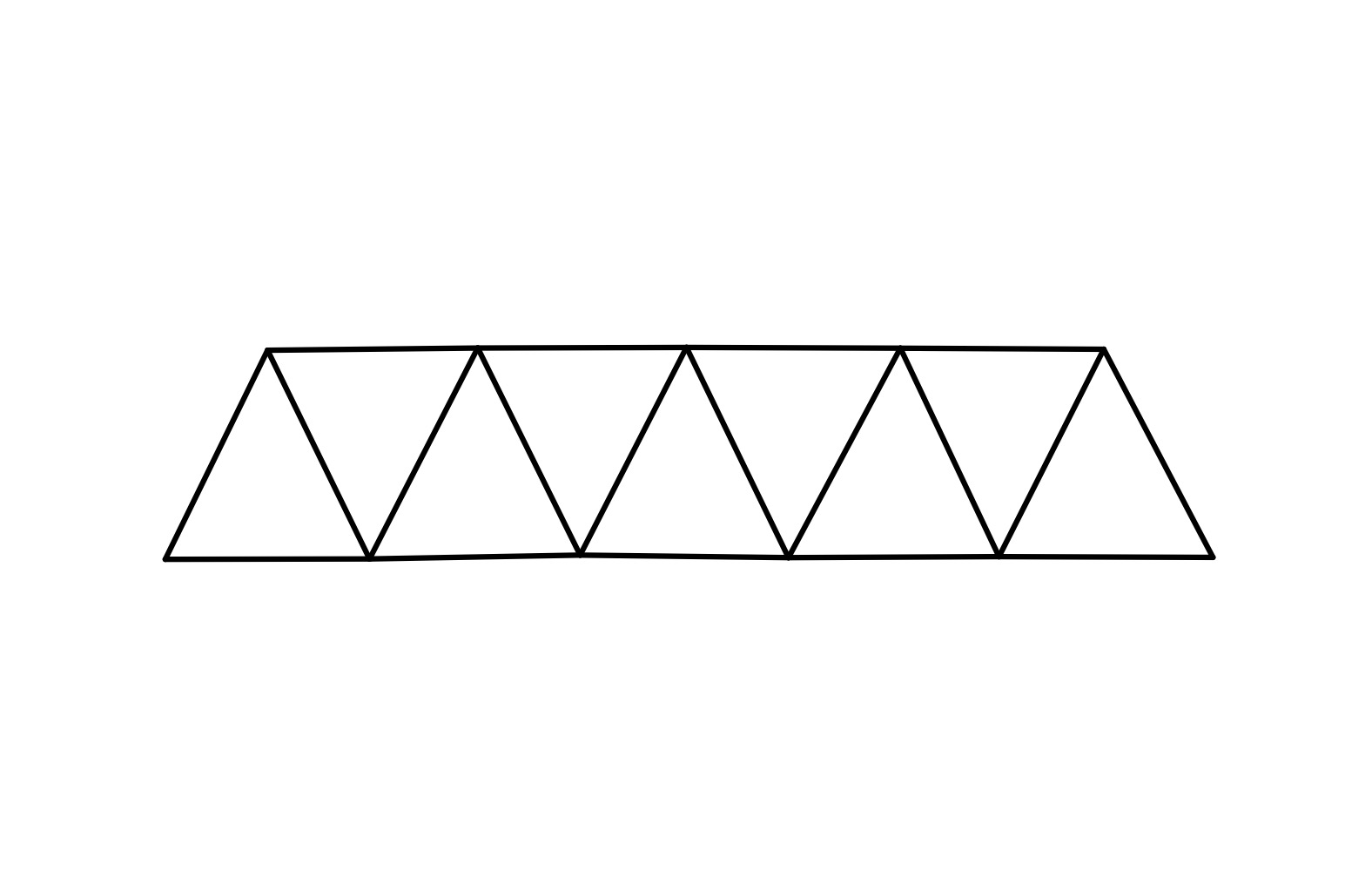
tops가 있는지 없는지 여부에 따라 위에 삼각형이 붙는지 안 붙는지가 결정된다.

그럼 첫 번째 예시에서는 tops가 [1, 1, 0, 1]로 주어졌기 때문에 세 번째를 제외한 나머지 부분에 삼각형이 붙었다는 사실을 확인할 수 있다.

이 그림은 다음과 같은 타일 네 가지로 붙여 넣을 수 있다.

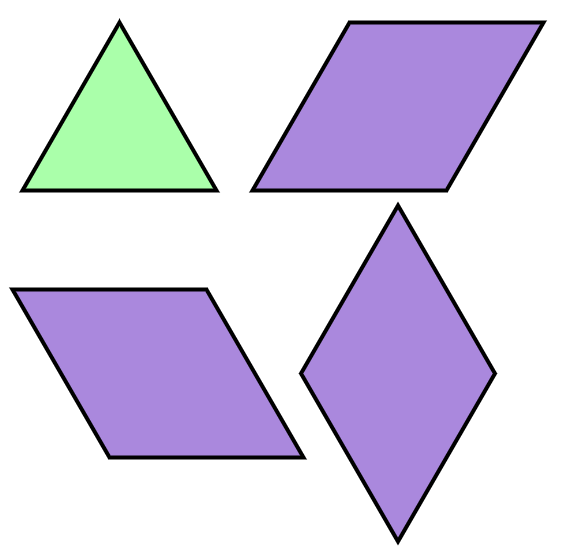
여기서 주의 깊게 보아야 하는 것은 네 번째 마름모 그림인데, 이는 위 tops가 존재할 때만 추가할 수 있다.

이런 식으로, 타일링 배치에 대한 규칙을 점화식으로 세울 수 있다.

반복되는 삼각형

다음 그림을 보자.

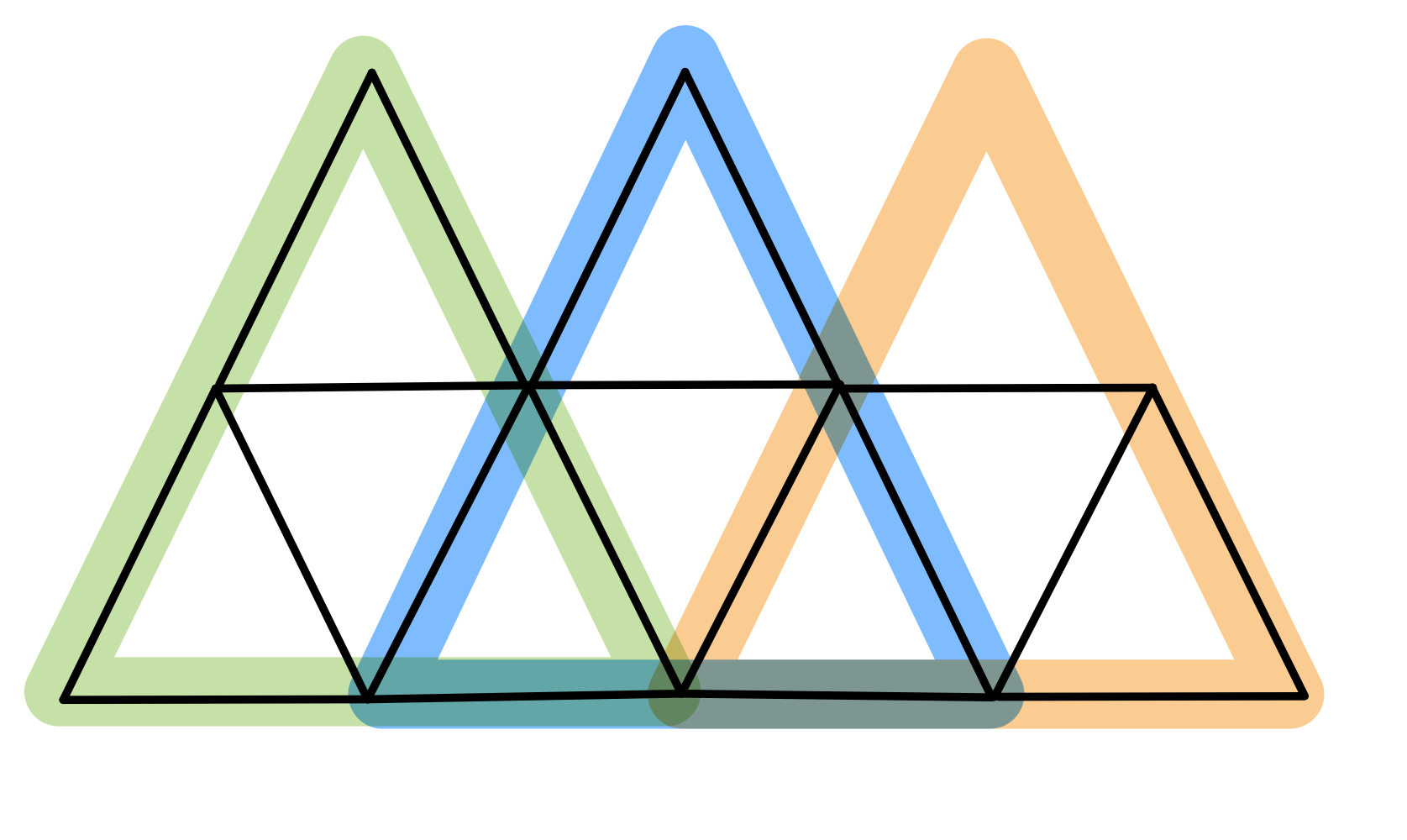
이처럼, 큰 삼각형이 반복되는 형태로 규칙이 나타나고 있음을 알 수 있다.

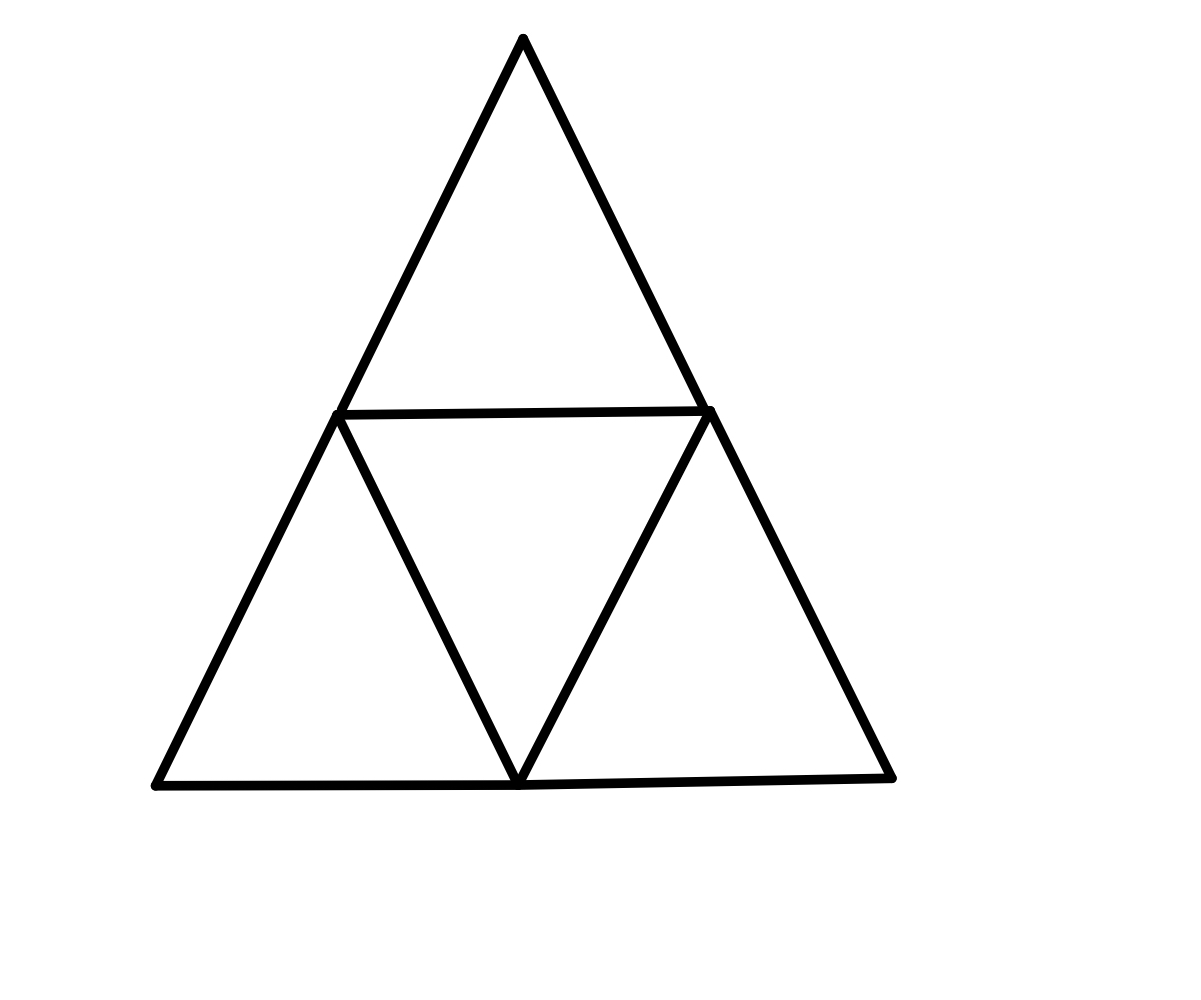
즉, 다음과 같은 삼각형에 배치를 파악한다면 그 이후 삼각형은 전 삼각형의 경우의 수에 현재 삼각형의 경우의 수를 곱하면 손쉽게 경우의 수를 파악할 수 있다.

여기서 주의 깊게 보아야 할 부분은 두 가지이다.

1. tops 존재 여부
2. 양쪽 겹쳐지는 삼각형

이제 진짜로 규칙을 구해보자.

타일링 규칙

규칙을 보기 앞서, 편의를 위해 삼각형에 번호를 매긴다.

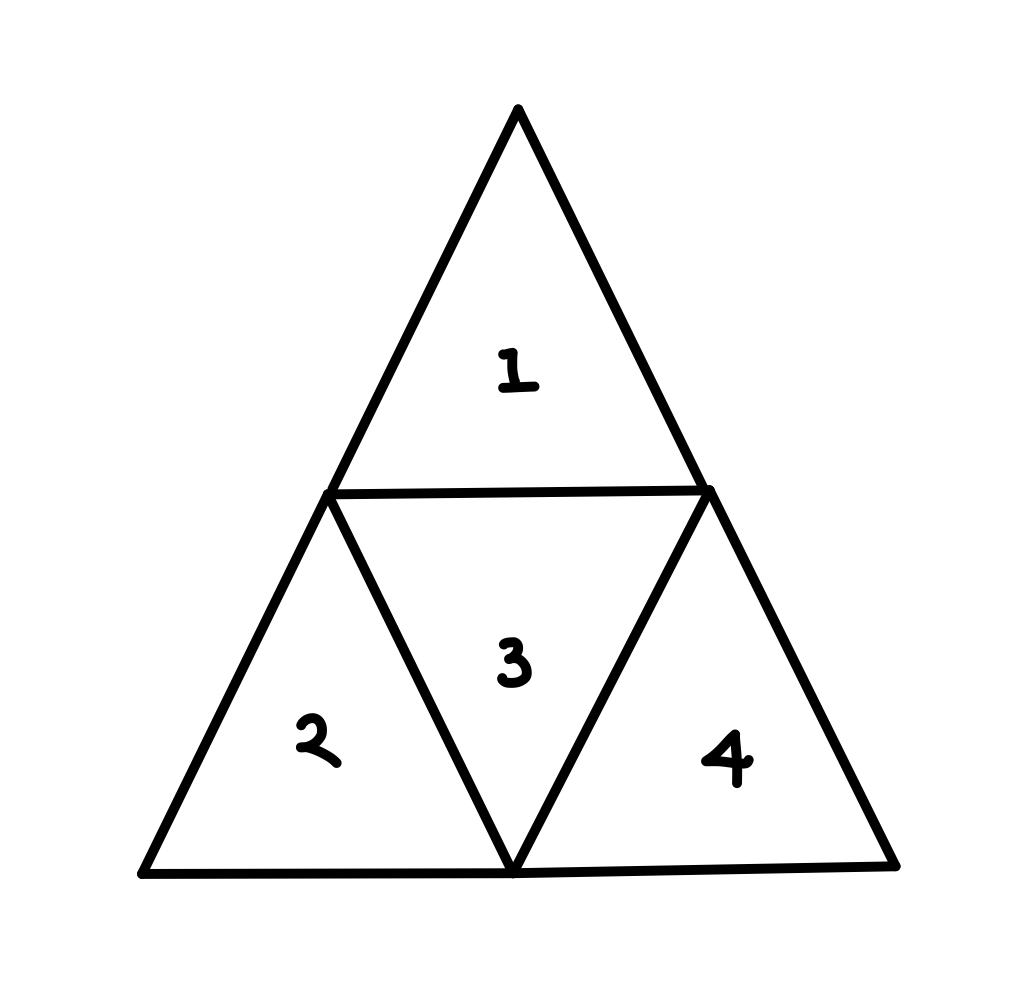
규칙은 다음과 같이 크게 두 가지로 나눌 수 있다.

1. tops가 존재하는가?
2. 4번 위치의 삼각형이 채워져 있는가?

만일 tops가 존재한다면 세로로 세워져 있는 마름모 타일(1, 3번 삼각형을 채울 수 있다.)을 배치할 수 있을 것이다.

2번은 고려할 필요가 없는 것이, 오른쪽으로 이동하기 때문에 2번은 결국 전 삼각형에서의 4번이 되기 때문에 4번 하나만 고려하는 것이다.

이를 a와 b로 나누어 2번 규칙의 경우의 수로 따지고자 한다. (4번 타일에 마름모 타일이 존재하는지 여부에 따른 분배)

• a[] : 4번 삼각형이 채워져 있는 경우의 수
• b[] : 4번 삼각형이 채워져 있지 않은 경우의 수

특히, a[]의 경우는 tops에 상관 없이 4번을 마름모 타일로 채워야 하므로 나머지 타일이 들어가지 못해 경우의 수는 한 가지라는 사실을 알아두자.

점화식

초기화는 다음과 같다.

• a[0] = 1 => (3, 4)
• (tops O) b[0] = 3 => (1, 3), (2, 3), (1, 2, 3)
• (tops X) b[0] = 2 => (2, 3), (2, 3)(타일 하나씩 채워져 있음)

점화식은 다음과 같다.

• a[i] = a[i-1] + b[i-1]
  => i번째 삼각형이 (2, 3)에 고정된 상태로 그 전 경우의 수를 다 더한다. (경우의 수를 모두 더해가며 dp[] 를 업데이트함으로써 기존 상태를 저장)

• (tops O) b[i] = 2 * a[i-1] + 3 * b[i-1]
• (tops X) b[i] = 2 * a[i-1] + 2 * b[i-1]
  => b[] 이므로 4번을 채워서는 안 된다.

점화식 설명

• tops O
  => 기존 삼각형이 a[i-1]로 2번이 채워져 있는 경우에는 (1, 3), (1, 3)(정삼각형 타일)로 경우의 수가 2이다.
  => 기존 삼각형이 b[i-1]로 2번이 채워져 있지 않은 경우에는 (1, 3), (2, 3), (1, 2, 3)로 경우의 수가 3이다.

• tops X
  => 기존 삼각형이 a[i-1]로 2번이 채워져 있는 경우에는 (1, 3)(정삼각형 타일)로 경우의 수가 1이다.
  => 기존 삼각형이 b[i-1]로 2번이 채워져 있지 않은 경우에는 (2, 3), (2, 3)(정삼각형 타일)로 경우의 수가 2이다.

코드

class Solution {
    public int solution(int n, int[] tops) {
        int[] a = new int[n];
        int[] b = new int[n];
        
        a[0] = 1;
        if (tops[0] == 1) b[0] = 3;
        else b[0] = 2;
        
        for (int i=1; i<n; i++) {
            a[i] = a[i-1]+b[i-1];
            if (tops[i] == 1) {
                b[i] = (a[i-1]*2 + b[i-1]*3) % 10007;
            } else b[i] = (a[i-1] + b[i-1]*2) % 10007;
        }
        
        return (a[n-1] + b[n-1]) % 10007;
    }
}

고려 사항

• 결과가 10007로 나눈 나머지를 구하라고 하였으니, 나누면서 배열을 업데이트한다.

참고 자료

• 2024 카카오 겨울 인턴십 코딩테스트 문제해설